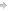И. А. Долгов, к. т. н. / А. В. Александров, к. т. н., ст. преп. Московский автомобильно-дорожный государственный технический университет (МАДИ)
ВВЕДЕНИЕ
В статье «Мобильный комплекс для регистрации и обработки параметров работы автомобильного двигателя», опубликованной в No 2 за 2017 год [1], сообщалось о разработке в лаборатории двигателей МАДИ датчиков для индицирования ДВС и о порядке обработки индикаторных диаграмм.
В настоящей статье демонстрируется возможность повысить достоверность результатов индицирования за счёт их сопоставления с результатами обработки сигнала датчика положения коленчатого вала, на основании которого можно рассчитать угловую скорость и ускорение коленчатого вала в каждый момент времени.
На первый взгляд, и работа четырёхтактного двигателя, и определение частоты вращения его вала — вещи тривиальные и не особо интересные, но мы постараемся рассказать об этом так, чтобы было интересно. Возможно, люди, считающие себя знакомыми с обозначенной проблематикой, найдут в материале что-то новое.
ОПИСАНИЕ ОБЪЕКТА
Принцип получения полезной механической работы в четырёхтактном поршневом ДВС достаточно прост: на сжатие относительно холодной топливовоздушной смеси работы затрачивается в несколько раз меньше, чем будет получено при расширении горячих продуктов сгорания. Теоретически для получения максимального КПД — максимального отношения полезной механической работы к затраченной химической энергии топлива — сгорание (подвод теплоты) должно происходить мгновенно при нахождении поршня в верхней мёртвой точке. Но физически это невозможно: процесс сгорания растянут во времени, и его протекание обусловлено рядом факторов (давлением, температурой, концентрацией компонентов, турбулизацией заряда, конфигурацией камеры сгорания). На процесс сгорания накладываются определённые граничные условия: уровень детонационного сгорания, образование токсичных компонентов.
Процессы, протекающие в поршневом двигателе, измеряются тысячными долями секунды: на номинальной частоте вращения рабочий цикл быстроходного бензинового двигателя (два оборота коленчатого вала) осуществляется за 20 мс, сгорание происходит за 1–2 мс. От протекания этого ключевого процесса зависят мощность и экономичность двигателя, поэтому анализу процесса сгорания уделяется большое внимание.
Традиционно основной контроль протекания сгорания осуществляется при помощи датчика давления, расположенного в камере сгорания. Процесс регистрации давления называется индицированием, зарегистрированное давление — индикаторной диаграммой. Зная давление в камере сгорания и площадь поршня, легко рассчитать усилие, с которым поршень действует на шатун; зная кинематику кривошипно-шатунного механизма, можно рассчитать крутящий момент, который генерирует процесс сгорания в конкретном цилиндре на коленчатом валу.
Основные выходные параметры ДВС — угловая скорость коленчатого вала и крутящий момент на нём, их перемножение даёт мощность двигателя.
Причиной изменения угловой скорости — углового ускорения коленчатого вала — является действующий на него суммарный крутящий момент.
КРУТЯЩИЕ МОМЕНТЫ, ДЕЙСТВУЮЩИЕ НА КОЛЕНЧАТЫЙ ВАЛ, И АНАЛИЗ ГЕНЕРИРУЮЩИХ ИХ ФАКТОРОВ
Коленчатый вал является интегрирующим звеном ДВС, воспринимает все силы, преобразует их в крутящие моменты, и, согласно второму закону Ньютона, его угловое ускорение в каждый момент времени должно подчиняться зависимости ε = ∑Mк / J*, где ε — угловое ускорение коленчатого вала; ∑Mк — суммарный крутящий момент, действующий на коленчатый вал; J* — момент инерции подвижных деталей ДВС, приведённый к оси вращения коленчатого вала.
Из этого следует, что если силы трения в ДВС отсутствуют, а к оси коленчатого вала приложить некий крутящий момент М, то угловое ускорение вала ε = M / J*. Момент инерции J* является константой для ДВС одной модели. Его точный расчёт представляется весьма трудоёмким, но он может быть определён с приемлемой погрешностью косвенными методами.
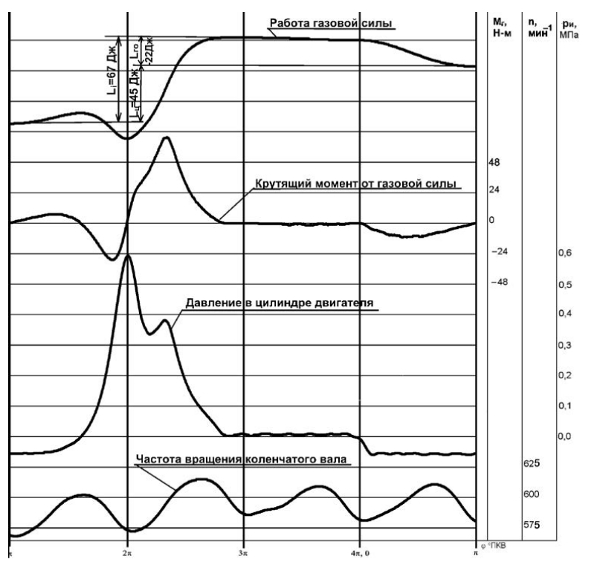
Рисунок 1. Пример регистрации давления в цилиндре ДВС, расчёта крутящего момента от газовой силы и её работы
Рассмотрим составляющие суммарного крутящего момента ∑M к . Прежде всего это крутящий момент от газовых сил M г . Как уже отмечалось, на оптимизацию этой составляющей направлена работа системы управления ДВС. На рис. 1 представлена зарегистрированная индикаторная диаграмма и рассчитанные на её основании параметры цикла — крутящий момент от газовой силы и её работа [3, 4]. Далее следует рассмотреть тормозящий момент от внешних сил: крутящий момент полезной нагрузки M пн — это то, ради чего работает двигатель. Если исключить из рассмотрения моменты переключения передач и разрыва кинематической связи колёс с дорогой при пробуксовке и преодолении неровностей, то есть основания полагать, что в остальных режимах работы автомобиля с гидромеханической трансмиссией М пн относительно стабилен, а на автомобиле с механической трансмиссией её упругие колебания превратят М пн в некоторую периодическую функцию. Насколько верны эти предположения, станет ясно в ходе анализа данных, зарегистрированных на движущемся автомобиле.
Теперь рассмотрим момент сил сопротивления M тр (t) — периодическую функцию, которая зависит от сил и относительной скорости перемещения деталей в ДВС. Силы, действующие в ДВС, являются функцией силы давления газов на поршень и сил инерции. При постоянной (на участке анализа данных, до 30 секунд) средней скорости вращения коленчатого вала можно считать, что M пн = M г – M тр .
Силы инерции М и возникают при изменении направления и скорости движения деталей, совершающих возвратно-поступательное и плоскопараллельное движение (поршней и шатунов). Момент от инерционных сил M и (t) — периодическая функция, которую можно рассчитать, зная кинематику кривошипно-шатунного механизма и массы поршней и шатунов.
Итак, можно сказать, что в любой момент времени ∑M к = M г + M пн + M и + M тр.
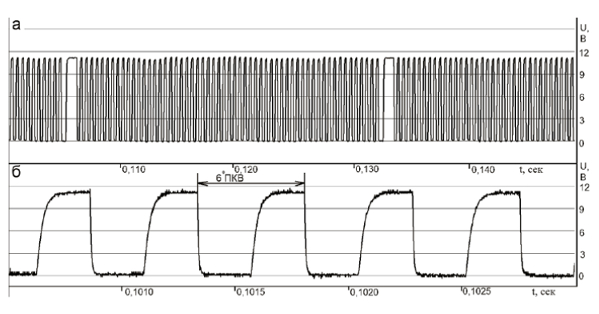
Рисунок 2. Сигнал ДПКВ, работающего на эффекте Холла; n = 2 100 мин –1
ПОСТАНОВКА ЗАДАЧИ
Индицирование ДВС — процесс дорогостоящий и трудоёмкий. При этом вопрос достоверности получаемых индикаторных диаграмм стоит достаточно остро. Тот факт, что при индицировании регистрируется сигнал датчика положения коленчатого вала, позволяет рассчитать левую часть равенства ε = ∑M к / J*, благодаря чему можно выйти на решение двух задач:
- повысить точность результатов индицирования ДВС за счёт сопоставления рассчитанного крутящего момента от газовых сил и углового ускорения коленчатого вала;
- на основании углового ускорения коленчатого вала смоделировать крутящий момент от газовых сил [2]. Сопоставление смоделированного крутящего момента и рассчитанного на основании индикаторных диаграмм позволит оценить возможную точность таких моделей.
ПЕРВИЧНАЯ ОБРАБОТКА СИГНАЛА ДПКВ
Рассчитать угловое ускорение коленчатого вала можно, обработав сигнал штатного датчика положения коленчатого вала (ДПКВ), взаимодействующего с инкрементным колесом, которое расположено на валу. Инкрементное колесо, именуемое 60-2, имеет 58 зубьев с угловым шагом 6° и свободный от зубьев сектор, сигнал от которого является реперным для системы управления двигателем. На рис. 2 представлен сигнал ДПКВ, работающего на основе эффекта Холла.
Величина, обратная времени прохождения одноимённых фронтов двух соседних зубьев, по сути, является средней угловой скоростью на участке 6° поворота коленчатого вала:
ῶ(t) = 1 / Δt ∙ k,
где ῶ — средняя угловая скорость коленчатого вала на участке 6°; Δt — время между одноимёнными фронтами зарегистрированного сигнала ДПКВ; k = 30 / π — коэффициент пересчёта.
В результате первичной обработки график скорости коленчатого вала ῶ(t) является дискретным и недифференцируемым, он представлен на рис. 3.
Рисунок 3. Результат первичной обработки сигнала ДПКВ — средняя угловая скорость на участке 6° ПКВ
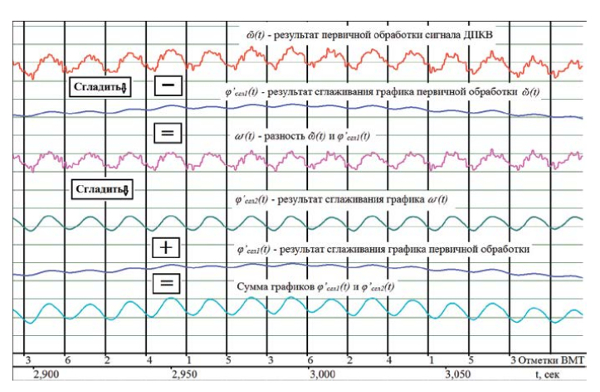
Рисунок 4. Иллюстрация работы математического алгоритма
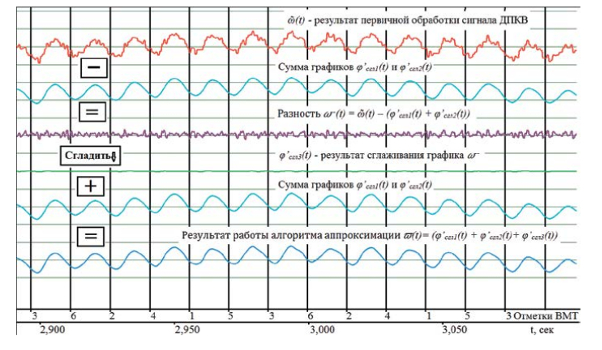
Рисунок 5. Итог работы алгоритма аппроксимации результатов первичной обработки сигнала ДПКВ
Однако такое представление противоречит физической сути рассматриваемого процесса: коленчатый вал с маховиком являются массивными деталями, и их ускорение ε(t) и скорость ω(t) должны быть непрерывными и гладкими.
АНАЛИЗ ЧАСТОТНЫХ СОСТАВЛЯЮЩИХ ФАКТОРОВ, ВЛИЯЮЩИХ НА УГЛОВУЮ СКОРОСТЬ И УСКОРЕНИЕ КОЛЕНЧАТОГО ВАЛА
Рабочий цикл четырехтактного ДВС осуществляется за 720 градусов поворота коленчатого вала. Основное влияние на ускорение коленчатого вала оказывает цилиндр, в котором заканчивается сжатие и начинается рабочий ход: в конце такта сжатия при подходе поршня к ВМТ коленчатый вал замедляется, а после прохождения ВМТ ускоряется. Процессы, одновременно происходящие в других цилиндрах двигателя, на ускорение коленчатого вала оказывают значительно меньшее влияние. Это обуславливает естественную периодичность колебаний угловой скорости. Для четырехцилиндрового двигателя зона преимущественного влияния одного цилиндра указана на рис. 3, её ширина составляет 180° ПКВ.
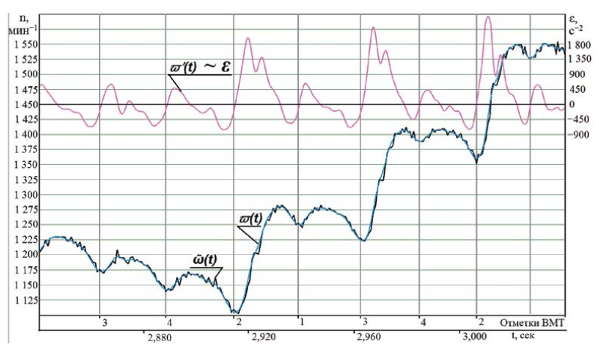
Рисунок 6. График угловой скорости ῶ(t), его аппроксимация π(t) и результат его дифференцирования π’(t) в начале свободного разгона при двух отключённых цилиндрах
Анализируя график угловой скорости ῶ(t) на значительном временном интервале, можно отметить, что он сформирован различными гармониками. Их условно можно разделить на несколько групп:
- инфранизкочастотные составляющие скорости коленчатого вала — результат десятков рабочих циклов с повышенной эффективностью (разгон, увеличение частоты вращения коленчатого вала) или пониженной (снижение частоты вращения, торможение двигателем);
- низкочастотные колебания скорости коленчатого вала в результате одного-двух рабочих циклов или пропусков зажигания;
- среднечастотные колебания скорости коленчатого вала на участке влияния рабочего процесса в одном цилиндре, отражающие особенности протекания процесса сгорания;
- высокочастотные колебания угловой скорости инкрементного колеса, вызванные крутильными колебаниями коленчатого вала;
- шум, вызванный неточностями при определении фронтов зубьев сигнала датчика положения коленчатого вала.
МАТЕМАТИЧЕСКИЙ АППАРАТ, ИСПОЛЬЗУЕМЫЙ ДЛЯ ДАЛЬНЕЙШЕЙ ОБРАБОТКИ СИГНАЛА ДПКВ
Для получения гладких скорости и ускорения коленчатого вала — π(t) и π’(t) — в программе обработки данных используются специально разработанные математические алгоритмы. Один из вариантов дальнейшей обработки сигнала ДПКВ — это разложение результатов первичной обработки в ряд Фурье с последующей фильтрацией определенных гармоник [5]. Но в последние годы в программе используется другой математический алгоритм: он позволяет обрабатывать весь зарегистрированный блок, не разбивая его на части.
На первом этапе этого алгоритма производится численное интегрирование (суммирование) результатов первичной обработки сигнала датчика положения коленчатого вала. В итоге получается зависимость угла поворота коленчатого вала от времени φ(t) и линейной интерполяции на участке 6° ПКВ между линиями одноименных фронтов. Затем полученный график φ(t) дифференцируется. Чем больше шаг дифференцирования, тем ниже частотная составляющая угловой скорости коленчатого вала, которая войдёт в итоговый результат φ’(t), — получается фильтр, отсекающий высокие частоты. На первом этапе график φ(t) дифференцируется, например, с шагом 10 мс. Полученный результат φ’ сгл1 (t) вычитается из исходного графика скорости ῶ(t). Разность ω - (t) = ῶ(t) – φ’ сгл1 (t) опять численно интегрируется, а затем дифференцируется, но уже с шагом 1 мс. Полученный массив обозначим φ’ сгл2 (t) и просуммируем с массивом φ’ сгл1 (t). Графики, полученные в результате этих действий, представлены на рис. 4.
Затем вычтем эту сумму из исходного массива: ῶ(t) – (φ’ сгл1 (t) + φ’ сгл2 (t)). Полученный массив, обозначенный ω -- (t), снова интегрируем и дифференцируем с шагом, например, 200 мкс. Полученный результат обозначим φ’ сгл3 (t). Затем просуммируем все три массива, полученные в результате дифференцирования, и обозначим результат π(t) = (φ’ сгл1 (t) + φ’ сгл2 (t) + φ’ сгл3 (t)). Полученный график скорости π(t) — гладкий и дифференцируемый. Критерием правдоподобности этого графика скорости коленчатого вала является близость результатов интегрирования графиков ῶ(t) и π(t), то есть хорошее соответствие угла поворота отметкам времени. Итог работы математического алгоритма представлен на рис. 5.
Для лучшего понимания представьте раллийный автомобиль, который движется по трассе с большим количеством контрольных пунктов. Известны расстояния между КП (шаг зубьев инкрементного колеса) и отметки времени прохождения. Если по этим данным построить график скорости, то получится кусочная функция, как на рис. 3. При этом скорость меняется мгновенно на границе участка, то есть ускорение автомобиля в этот момент оказывается нереалистичным. Если нам удаётся получить плавный график скорости автомобиля с правдоподобными ускорениями и отметками времени на КП (интеграл скорости движения автомобиля), соответствующими реальному автомобилю, то задачу нахождения реальной скорости автомобиля в каждый момент времени можно считать решенной с некоторой точностью. Естественно, точность зависит от частоты следования КП и характеристик автомобиля (максимально возможное ускорение и замедление).
Используемый в программе обработки алгоритм фильтрации исходного графика скорости несколько отличается от приведённого: в нём большее число итераций, а шаг дифференцирования в каждой итерации меняется в зависимости от угловой скорости коленчатого вала. Вариацией шага дифференцирования можно влиять на график π(t) и его производную π’(t), по сути, являющуюся ускорением коленчатого вала ε. Близость результатов интегрирования графиков ῶ(t) и π(t) не исключает некоторых отличий реального ускорения коленчатого вала от результатов дифференцирования графика π(t), поэтому совершенствование алгоритма обработки сигнала ДПКВ является одной из первоочередных задач на пути к поставленной цели.
На рис. 6 представлены два последовательных рабочих цикла двигателя в момент начала свободного разгона, 1-й и 4-й цилиндры не работают. Для удобства восприятия график ῶ(t) состоит не из горизонтальных, а из наклонных линий, соединяющих середины участков между фронтами сигнала ДПКВ.
Очевидно, что отличия в протекании рабочего процесса — закона изменения давления в цилиндрах двигателя — отражаются на угловой скорости и ускорении коленчатого вала, но насколько эта связь жёсткая и как точно её можно отследить?
СПИСОК ЛИТЕРАТУРЫ:
- Долгов И. А. Мобильный комплекс для регистрации и обработки параметров работы автомобильного двигателя / И. А. Долгов, А. В. Александров // Журнал автомобильных инженеров. — 2017. — No 2 (103). — С. 11–17.
- Долгов И. А. Актуальность индицирования ДВС / И. А. Долгов, А. В. Александров // Журнал автомобильных инженеров. — 2016. — No 5 (100). — С. 19–23.
- Александров А. В. Методические основы разработки диагностического комплекса для оценки технического состояния автомобильных двигателей: дис. ... канд. техн. наук. — М.: МАДИ, 2013.
- Александров А. В. Методические основы разработки диагностического комплекса для оценки технического состояния автомобильных двигателей: автореф. дис. ... канд. техн. наук. — М.: МАДИ, 2013.
- Александров А. В. Согласование параметров сигналов первичных преобразователей и проверка достоверности полученных данных при проведении углубленной диагностики двигателей внутреннего сгорания / А. В. Александров, И. А. Долгов // Вестник Московского автомобильно-дорожного государственного технического университета (МАДИ). — 2012. — No 2. — С. 50– 56.



 Диагностика автомобилей
Диагностика автомобилей